Np-Urのデータ分析教室

オーブンソースデータなどWeb上から入手できるデータを用いて、RとPython両方使って分析した結果を書いていきます

トップ > Pythonで実践編 > PythonのStatsModelsによる線形回帰分析! 交差項もモデルに入れてみた!

PythonのStatsModelsによる線形回帰分析! 交差項もモデルに入れてみた!

Pythonで実践編 線形回帰

今回は、Pythonを使って実際に重回帰分析をしていきたいと思います。
回帰分析って何？という方はこちらの記事を参考にしてみてください。
randpy.hatenablog.com

データの傍観

Pythonにはscikit-learnという機械学習によく使われるライブラリがあります。クラスタリングや分類、回帰など網羅していて、機械学習を始める方にはうってつけのライブラリです。

そんなscikit-learnには、無料で使えるデータセットが備わっています。
今回は、その中からbostonの住宅価格のデータを使ってみたいと思います。正直面白いデータセットではないかも知れませんが、これを参考に今後色々なデータに対して回帰分析をして頂けたらと思います。

さっそく、どのようなデータセットになっているのか見ていきましょう！

import pandas as pd
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
#住宅価格のデータを追加する
df['Price'] = boston.target
#先頭5行だけ表示
df.head()

f:id:gl2000-sans:20170621103659p:plain
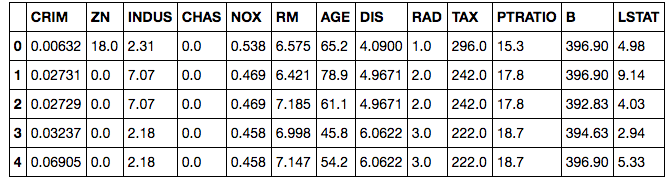
きちんとデータが読み込まれていますね。
pd.DataFrameでデータフレームとしてデータを読み込みます。columnsでカラム名の指定をしましょう。
データセットの詳細は以下コマンドで見ることができます。

print(boston.DESCR)

f:id:gl2000-sans:20170621104613p:plain

犯罪率や部屋の数など色々なデータが入っていますね。
データを傍観する際は、色々な仮説を立てる癖をつけるといいと思います。
例えば、犯罪率が高いと住宅価格は下がりそうだなとか、部屋の数が増えると上がりそうだなみたいな感じです。
実際に分析して、仮説の検証をするのはデータ分析の醍醐味ですよ！

さて、データの数字だけ見ていてもよく分からないので、可視化してみましょう。
Pythonでの可視化ツールとしては、matplotlibとseabornが有名です。（というか、この二つだけあればとりあえず十分！）

試しに部屋の数と価格の散布図とヒストグラムを見てみましょう。散布図を見るためにseabornのjointplotを使用します。
jupyter notebookを使用している場合は、必ず以下のように、%matplotlib inlineを忘れずに書きましょう！これ書かないと表示できません。

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.jointplot('RM', 'Price', data=df)

f:id:gl2000-sans:20170623104746p:plain

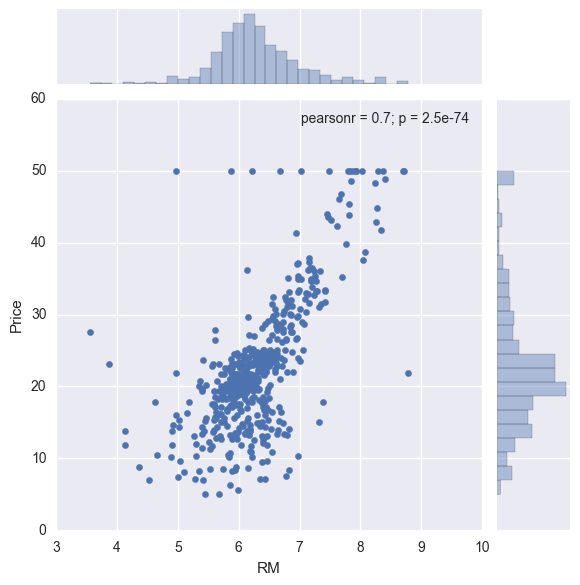
jointplotでは、散布図とヒストグラム、ピアソンの積率相関係数を出してくれます。ヴィジュアル的にもなかなかいけてます！
さて、散布図を見ていただけたらわかると思いますが、部屋の数が増えるとともに、住宅価格が上がってっていますね。
仮説通りデータの分布もそのような形になっているようです。（直感的にもあってそうですね）
相関係数も0.7と高い値で、帰無仮説も棄却されています。

さて、住宅価格のヒストグラムに注目していただくと（右側）、ばらつきは多少ありますが、20＄付近を中心とした正規分布の形になっているため、線形回帰分析でよさそうです。
正規分布について詳しく知りたい方は以下記事を参考にしてみてください。
randpy.hatenablog.com

二つの変数だけでなく、一気に全変数間の散布図を見たいときは、seabornのpairplotがオススメです。
kindの部分で回帰直線も引いてくれるよう設定できます。

sns.pairplot(df, kind = "reg")

f:id:gl2000-sans:20170623110411p:plain

はい。変数が多すぎて全くわかりません(笑)
変数全部ではなく、一部の変数を指定したい場合は"vars = "で設定しましょう。

sns.pairplot(df, kind = "reg", vars = ["Price", "RM", "DIS"])

f:id:gl2000-sans:20170623110832p:plain

いやーseabornいけてますね！（何回言ってるんだろ、、）
さて、scikit-learnには、他にも使えるデータセットはいくつかあるので、詳しく知りたい方はこちらを参考にしてみください。
http://scikit-learn.org/stable/datasets/

パッケージ"statsmodels"の勧め

Pythonで回帰分析をするパッケージはいくつかあり、機械学習のライブラリとして有名なscikit-learnや、pandasにあるメソッドでも分析は行えます。
しかし、上記ライブラリでは、P値*1やダービンワトソン比*2をデフォルトで出してくれません。例えば、P値を算出しないと、統計的有意性があるのかどうか分からず、結果への信頼性に関わってきます。

ここでお勧めしたいのがstatsmodelsです。
statsmodelsでは、統計分析パッケージで、時系列分析や一般化線形モデルなど様々な分析モデルに対応しています。

ただし、Rほどパッケージや機能は充実していないので、応用して何か分析するとなったら自分でコーディングする必要がでてきますが、
普通の分析をするならこれだけあれば十分です。

詳細は以下ドキュメントをご参照ください。
http://www.statsmodels.org/stable/index.html

実践編

さて、データも整ったので、実際に分析をしていきましょう。
線形回帰は簡単で、statsmodelsの"formura.api"をimportして頂いて、"smf.OLS()"でモデルを定義し、メソッド"fit()"で完了です。(笑)

推定はsmf.OLSの部分でOLSを指定してますが、WLS（重み付き最小2乗法）なども指定できます。
ちなみに、formula.apiでは、Rのような記述をすることができるので、smf.ols(formura = '目的変数名~ 説明変数', data = data)のように記述することも可能です。

R仕様で使う場合はメソッドとして小文字の"ols"を使用しますのでご注意ください。

import statsmodels.formula.api as smf
#説明変数
X = df.drop('Price',1)
#目的変数
Y = boston.target
model = smf.OLS(Y,X)
result = model.fit()
result.summary()

result.summary()で分析結果について見ていきましょう。

OLS Regression Results
Dep. Variable:	y	R-squared:	0.959
Model:	OLS	Adj. R-squared:	0.958
Method:	Least Squares	F-statistic:	891.1
Date:	Mon, 26 Jun 2017	Prob (F-statistic):	0.00
Time:	09:50:02	Log-Likelihood:	-1523.8
No. Observations:	506	AIC:	3074.
Df Residuals:	493	BIC:	3129.
Df Model:	13		
Covariance Type:	nonrobust		
coef	std err	t	P>|t|	[95.0% Conf. Int.]
CRIM	-0.0916	0.034	-2.675	0.008	-0.159 -0.024
ZN	0.0487	0.014	3.379	0.001	0.020 0.077
INDUS	-0.0038	0.064	-0.059	0.953	-0.130 0.123
CHAS	2.8564	0.904	3.160	0.002	1.080 4.633
NOX	-2.8808	3.359	-0.858	0.392	-9.481 3.720
RM	5.9252	0.309	19.168	0.000	5.318 6.533
AGE	-0.0072	0.014	-0.523	0.601	-0.034 0.020
DIS	-0.9680	0.196	-4.947	0.000	-1.352 -0.584
RAD	0.1704	0.067	2.554	0.011	0.039 0.302
TAX	-0.0094	0.004	-2.393	0.017	-0.017 -0.002
PTRATIO	-0.3924	0.110	-3.571	0.000	-0.608 -0.177
B	0.0150	0.003	5.561	0.000	0.010 0.020
LSTAT	-0.4170	0.051	-8.214	0.000	-0.517 -0.317
Omnibus:	204.050	Durbin-Watson:	0.999
Prob(Omnibus):	0.000	Jarque-Bera (JB):	1372.527
Skew:	1.609	Prob(JB):	9.11e-299
Kurtosis:	10.399	Cond. No.	8.50e+03

色々な値がでてきましたね。

全ての統計量について理解するのは大変なので、説明変数が並んだ各列についてのみ説明していきます。
まぁとりあえずここの数字が読み取れれば、分析の考察はできるので。
左から順に、

  • coef : 偏回帰係数。OLSで求めたパラメータ値
  • std err : パラメータの標準誤差。ばらつきがあるのかどうか
  • t : 有意かどうかの際に用いる値
  • P>|t|：推定されたパラメータがゼロである確率
  • [95.0% Conf. Int.]：95％信頼区間。95％の確率でこの区間内に値が収まる

ここで注目したいのが、P値の部分です。ここの値が0.1より小さければ、有意水準10%で有意となります。
有意水準は10%,5%,1%がよく使われており、一般にこれらの有意水準よりも小さな値になれば、統計的に信頼できる結果であると結論づけることが多いです。

さて、分析結果を見ていくと、
例えば、CRIM（犯罪率）は、マイナスに1%有意な結果です。犯罪率が1%高くなると住宅価格は0.0916$下がるとなっています。直感的にもマイナスになっているのはあってますね。（犯罪率が高い→需要が減る→価格が下がる）

RM（部屋の数）は正に有意、DIS（5つの雇用施設からの距離）は負に有意となっており、部屋の数が増えると住宅価格の値段が高くなり、都心から距離が離れると価格は下がるということを示しており、これらの変数も納得いく結果がでています。

交差項の導入

さて、少し発展として交差項をモデルに追加してみましょう。
例えば、先ほどの分析結果からもわかる通り、都心からの距離が遠くなるほど価格は下がり、部屋の数が増えるほど価格は上がります。
さて、ここで考えていただきたいのは、部屋の限界効果（1部屋増えた時の住宅価格の上昇率）というのは、都心からの距離にかかわらず一定なのでしょうか？予想としては、都心に近いほど、1部屋増えた時の住宅価格の上昇率は大きそうな気がします。例えば、渋谷で1LDKから2LDKに変わるときの家賃上昇率と八王子で1LDKから2LDKに変わるときの家賃上昇率を考えると、渋谷のほうが１部屋増えたときの上昇率はおそらく高くなるでしょう。

そういった影響を見るために交差項というのを導入します。
導入方法は簡単で、説明変数に次の項を追加するだけでその効果が見れます。
$$
Y = αRM+βDIS+γ(RM*DIS)+ε
$$
γ(RM*DIS)の部分が交差項になります。（RM：部屋の数、DIS：都心からの距離）
さて、交差項の効果を見るために、上記式をRMで偏微分してみたいと思います。
$$
\frac{\partial Y}{\partial RM} = α + γ*DIS
$$
式を見ていただくと、部屋の数の価格への限界効果が、距離(DIS)によって変化していることがわかります。
距離が遠くなる程、限界効果が下がっていくはずなので、γの符号はマイナスであることが予想されます。

さて、実際に交差項を追加してOLSをしてみたいと思います。

#RMとDISの交差項の追加
X['RM_DIS'] = X['RM'] * X['DIS']
model = smf.OLS(Y,X)
result = model.fit()
result.summary()

OLS Regression Results
Dep. Variable:	y	R-squared:	0.959
Model:	OLS	Adj. R-squared:	0.958
Method:	Least Squares	F-statistic:	828.4
Date:	Mon, 26 Jun 2017	Prob (F-statistic):	0.00
Time:	10:40:37	Log-Likelihood:	-1523.1
No. Observations:	506	AIC:	3074.
Df Residuals:	492	BIC:	3133.
Df Model:	14		
Covariance Type:	nonrobust		
coef	std err	t	P>|t|	[95.0% Conf. Int.]
CRIM	-0.0928	0.034	-2.708	0.007	-0.160 -0.025
ZN	0.0446	0.015	3.018	0.003	0.016 0.074
INDUS	-0.0084	0.065	-0.130	0.896	-0.135 0.118
CHAS	2.8834	0.904	3.190	0.002	1.108 4.659
NOX	-1.6175	3.508	-0.461	0.645	-8.511 5.276
RM	5.5515	0.431	12.868	0.000	4.704 6.399
AGE	-0.0063	0.014	-0.453	0.651	-0.033 0.021
DIS	-2.0786	0.916	-2.269	0.024	-3.879 -0.279
RAD	0.1572	0.068	2.328	0.020	0.025 0.290
TAX	-0.0092	0.004	-2.337	0.020	-0.017 -0.001
PTRATIO	-0.3307	0.121	-2.743	0.006	-0.568 -0.094
B	0.0154	0.003	5.678	0.000	0.010 0.021
LSTAT	-0.4084	0.051	-7.977	0.000	-0.509 -0.308
RM_DIS	0.1874	0.151	1.241	0.215	-0.109 0.484
Omnibus:	205.078	Durbin-Watson:	0.978
Prob(Omnibus):	0.000	Jarque-Bera (JB):	1405.803
Skew:	1.612	Prob(JB):	5.42e-306
Kurtosis:	10.502	Cond. No.	8.92e+03

RM_DISが交差項になりますが、仮説とは逆にプラスになっています。まぁ有意ではありませんが、、、
ちょっとここで、どうしてこのような結果になってしまったか原因を探るために、RM,DIS,Priceのプロットを見てみましょうか。
f:id:gl2000-sans:20170623110832p:plain
そもそも距離が遠くなる程、価格は上昇傾向にあるみたいです。（一番右上の図）
また、DISの定義が5つの雇用施設からの重み付き距離になっているので、この指標自体が厳密には都心からの距離を表しているわけではないため、このような結果になっているのかもしれません、、、

まぁ、仮説通りの結果が得られないことの方が多いので、この辺りは試行錯誤の余地があるのかなと思います。

さいごに

いかがだったでしょうか。
案外、コードの記述量も少ないし簡単にできるなという印象を持って頂ければ幸いです。

今回の一通りの流れで簡単な分析はもうできると思いますので、自分で興味のあるデータを集めて分析してみるといいと思います。
WEBデータの収集としてスクレイピングという技術がありますがそれについては、こちらの記事で紹介してます。
randpy.hatenablog.com

コードはRですが、Pythonでもスクレイピングはできるので、機会があればPythonによるスクレイピング記事も書きたいなと思います。
次回は一般化線形モデル、非線形回帰の理論、実践編について執筆する予定ですのでお楽しみにー！

Pythonによるデータ分析入門 ―NumPy、pandasを使ったデータ処理

Pythonによるデータ分析入門 ―NumPy、pandasを使ったデータ処理

Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)

Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)

*1:P値とは偏回帰係数がゼロである確率

*2:系列相関の検定