都議選のデータ使ってPythonでロジスティック回帰分析　都民ファーストがやっぱり最強か!?

今回は、前回習った一般化線形モデルの実践編です。
理論編については、以下記事を参考にしてください。
randpy.hatenablog.com

分析テーマは、この前行われた都議選です！！

立候補者のどのような属性が当選確率に影響したのか、ロジスティック回帰分析を使って求めてみたいと思います。

まぁおそらく、どの政党に所属しているかどうかが一番変数として効いてきそうな気がしますが、それも実際に分析して検証していきましょう。

今回の記事の流れとしては、

PythonでWebスクレイピング
ロジスティック回帰分析

このように進めていきます。
webスクレイピングについては、今度詳細な記事を出したいと思いますので、今回は軽めの説明に止まりますが、ご了承くださいませ。（スクレイピングについては勉強不足な部分も多いので、、、）

Beautiful Soupによるwebスクレイピング

Pythonでwebスクレイピングをするためのパッケージは幾つかありますが、今回はその中でも代表的なBeautiful Soupを使って、サイト上の必要なデータを取ってきたいと思います！
まだBeautiful Soupをインストールしていない方は、以下のコマンドを実行してインストールしましょう。

pip install beautifulsoup4

今回の分析では、説明変数として立候補者の属性（年齢、政党、当選回数など）と、目的変数として当選したかどうかのデータを用います。
それぞれデータのソースが異なるので、別々に取得していきます。

説明変数の取得

以下URLから立候補者の属性データをとってきたいと思います。
党派別立候補者数:都議選２０１７:東京新聞(TOKYO Web)

属性としては、年齢・所属・当選回数などです。正直、説明変数としては不十分だとは思いますが、使えそうな変数が見つからなかったので、今回はこれで分析を進めます。

以下がPythonコードの一覧になります。コードをピックアップして要所要所、説明していきます。
https://github.com/tk2133/data_analytics/blob/master/scrapy/scrapy_senkyo.py
（正直、とてつもなく汚いコードが出来上がってしまいました、あまり参考にしないほうがいいです！笑　後ほど時間があるときにリファクタリングします…）

9行目：地区ごとにURLが分かれているので、そのURLリストを生成する関数を定義
10行目~11行目：request.get(URL)で、HTMLを読み込んであげ、beautifulsoupに渡すことで、タグの抽出などができるようになります。

ちなみに、スクレイピングしていると必ずエンコードの問題に行き当たって、文字化けすることが多いかと思います。そして、いちいち対応するのが正直めんどくさいです。
色々調べてみましたが、こちらの記事を参考にして文字化けの問題を解決しました。（普通にやったら文字化けします、、、）
RequestsとBeautiful Soupでのスクレイピング時に文字化けを減らす - orangain flavor

基本的には、Chardetをインストールして、9~10行目のコードを書けば、かなり文字化けを減らせるそうなので、文字化けに悩んでいた方は試してみてください。

12~18行目：findメソッドを使うことで、HTML内のタグを指定（classなど複数指定できる）して、必要な箇所の情報を抽出できます。find_allでは、HTML内で、指定した全てのタグを引っ張ってこれます。

17行目：タグに挟まれたテキストを取得する場合は、タグを指定したうえでtextメソッドを使います。リンクのURLなどは、タグ内にあることが多いと思いますが(< a href = ~>)、その場合はattrsメソッドを使用します。ここでは、地区名とURLを辞書の形で保存するようにしています。{'千代田区':'URL', '大田区' : 'URL' ,・・・}

21行目：URLから立候補者の属性を抽出し、データフレームとして保存する関数を定義しています。

23~28行目：先ほどと同様に、HTMLのタグを検索して必要な箇所をピックアップしています。26行目では、選挙区の定数と立候補者数が一つの文字列になっていたので、re.splitを使って、定数と立候補者数の二つに分割してあげてます。

30~43行目：タグ内のデータが規則的に現れる(名前→年齢→政党→・・・）ので、それに合わせて、データフレームに保存するようにしています。この辺は特にコードが汚いです。。

スクレイピング経験がほぼほぼ無かったのですが、やっぱり慣れないと難しいですね。。。
（ある程度自分の中で整理できた段階でスクレイピングの記事を出したいと思いますので今回は勘弁してください…。）

目的変数の取得

目的変数としては、候補者が当選したかどうか(0 or 1)の情報を使用します。
以下のサイトからデータを取得しました。当選者の名前のリストを作ってあげて、あとで説明変数のデータフレームに追加してあげます
開票速報（世田谷区）- 2017都議選：朝日新聞デジタル

こちらも先ほどのスクリプトとそれほど変わらないので、
割愛しますが、全コードは以下リンクから参照できるようにしておきます。
https://github.com/tk2133/data_analytics/blob/master/scrapy/scrapy_senkyo_endo.py

初めからこちらのサイトでスクレイピングすれば、説明変数と目的変数両方取ってくることができたことに後から気づくというね、、、、

ロジスティック回帰分析

さぁ無事に？データを取得できたので、さっそくロジスティック回帰をしていきましょう！

sklearnでもロジスティック回帰はできますが、推定結果の考察をするための統計指標を出してくれないので、今回もstatsmodelsを利用したいと思います。
statsmodelsによるロジスティック回帰の方法は以下の2通りありますが、

statsmodels.Logit
statsmodels.glm

今回はlogitのモジュールを使って分析してみます。

statsmodelsのGLMのメソッドで、リンク関数にベルヌーイ分布を仮定しても同じ結果が得られますので、試してみてください。

まずは、前処理で、先ほど取得したデータを結合していきます。

import pandas as pd
import csv
#説明変数のデータをimport
df = pd.read_csv(path + 'dataset_senkyo.csv')

#当選者リストのデータをimport
win_list = []
with open(path + 'win_list.tsv', 'r') as f:
    reader = csv.reader(f, delimiter = '\t')
    for name in reader:
        win_list.append(name[0])

#説明変数のデータフレームに目的変数を追加
for i in range(len(df)):
    if df.loc[i,'name'] in win_list:
        df.loc[i,'win'] = 1
    else:
        df.loc[i,'win'] = 0

当選者リストの名前と、説明変数のデータの中の名前が一致したらflg = 1を立ててあげるようにして目的変数を作成します。
目的変数（カラム名'win'）としては、当選したら1、非当選なら0の2値になります。
データセットは以下のようなイメージです。
f:id:gl2000-sans:20170713131801p:plain

さて、見て頂くとわかる通り、affiliation,statusなどに入っている値は文字列（質的変数と言ったりします）となっており、このままでは分析できません。

このような場合はダミー変数というものを導入して、モデルに取り入れます。
例えば、性別のダミー変数を作る場合は、（男性なら１、女性なら0）といった感じで数値に変換してあげます。

さて、性別はカテゴリが2つだったので、0,1で表すことができましたが、3つ以上の場合はどうするの？と疑問に思うかと思います。
3つ以上の場合、例えば自民党、民進党、都民ファーストの3つを考えてみると、この場合は民進党ダミー（民進党なら1,それ以外は0）と都民ダミー（都民ファーストなら1,それ以外は0）の2つの変数だけ導入します。

3つカテゴリがあるのに何で2つでいいの？と思ったかと思いますが、実は、自民党は二つの変数で表すことができています。（民進党＝0かつ都民ダミー＝0　→　ということは自民党所属）
ここにあえて自民党ダミーを入れてしまうと、完全な多重共線性（ある説明変数が他の説明変数の線形和で表せる）が生まれてしまい推定結果が不安定になるため、基準となるダミー変数は普通は入れません。

ダミー変数の解釈ですが、「基準となるカテゴリ（＝自民党）と比べて、民進党、都民ファーストに所属していたとき、当選確率はどう変化するのか」という風になります。

さて、実際にダミー変数を作成していきましょう！

#説明変数、目的変数
X = df.drop('win',1)
Y = df['win']

#ダミー変数作成
dummy_df = pd.get_dummies(X[['affiliation', 'status']], drop_first = True)
df2 = pd.merge(X, dummy_df, left_index=True, right_index=True)
X = df2.drop(['area', 'carrer','affiliation', 'recommend', 'status','name','teisu','number'],1)

pandasのget_dummiesを使うことで簡単にダミー変数を作成することができます。
drop_first = Trueとすることで、基準となるダミー変数は作成しないよう設定できます。

ちなみに、今回は収集したデータを全て使わず、一部分を使って推定しています。（職業など含めると説明変数が多くなりすぎてしまうため。）
また、モデルに入れる変数選択の方法については最後に少しだけ触れたいと思います。

あとは、pandasのmergeを使い、indexをkeyとしてXとdummy_dfを結合してあげます。
f:id:gl2000-sans:20170713154627p:plain
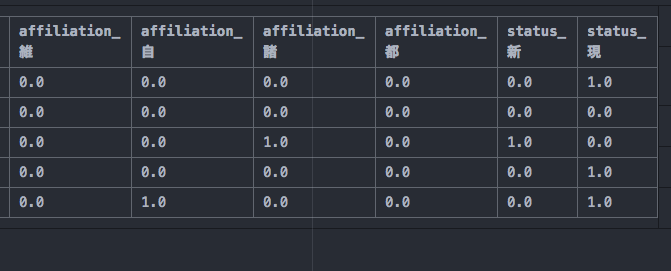
無事にダミー変数化できているようです。

さぁデータ整形が終わりましたので、いよいよ分析していきます！ここまで長かった笑
データ分析というとカッコイイ印象を持つ方も多いかもしれませんが、大部分はこのような泥臭いデータの前処理によって時間が消費していきます。辛い…。

statsmodels.apiの中のLogitというメソッドを使います。分析の流れは線形回帰のときと同様で、まずモデルを定義(sm.Logit(Y,X))してあげて、そのあとfitを使って推定します。sklearnも含めてだいたいこの方式なので慣れておくといいと思います。'method'の部分では、最尤法のアルゴリズムの指定をしています。

# Logit Model
import statsmodels.api as sm
logit = sm.Logit(Y, X)
result = logit.fit(method='bfgs')
result.summary2()

推定結果をみていきましょう！
f:id:gl2000-sans:20170713141321p:plain

推定結果の見方（表のカラムの意味）は線形回帰分析のときに説明した通りなので、もし分からないよというかたは、こちらを参考にしてみてください。
randpy.hatenablog.com

さて、有意になっている変数を見てみると、年齢、公明党ダミー、都民ファーストダミー、status(現職かそうでないか）の4つになります。
ageがマイナスになっているので、若手であるほど当選しやすいことが分かります。また、やはり都民ファーストに所属しているだけでかなりオッズは高くなるようです。
オッズとは、当選確率を落選確率で割った値を指しています。
$$\frac{q_i}{1-q_i}$$
式にすると上のようになります。要は、当選確率が上がるほどオッズは上がり、当選確率が下がるほどオッズは下がります。

実際にオッズが何倍になっているのか計算してみましょう。
線形回帰分析のときとは違って、推定された係数から直接オッズへの影響をみれないので注意してください。
randpy.hatenablog.com

の方で、理論の説明をしましたが、以下のようなモデル式をロジスティック回帰では推定しています。
\begin{eqnarray*}
\log \frac{q_i}{1-q_i} = a + b x_i
\end{eqnarray*}

なので、両辺のexpをとってあげれば、左辺の対数が外れる（=オッズになる）ため、推定した係数を元にオッズがどれだけ変化するのか計算することができます。
都民ファーストダミーの推定値のexpをとってあげると、exp(6.1328)なので、オッズがだいたい460倍高くなるという結果です。
数字を見ても都民ファーストがどれだけすごかったかのかが分かりますね。

最後に

今回はとりあえずロジスティク回帰をまわしてみるという段階で終わってしまいましたが、実際にはもっと考慮しなければいけないことはたくさんあります。

例えばそもそも説明変数が少ないので、性別やTwitterでの情報発信の有無など入れると面白い結果が生まれるかもしれません。
他には、AICという情報量基準を用いてモデルの選択を行ったり、最尤法のアルゴリズムを変えてみたり（今回は準ニュートン法）色々できることはあるので、今後も追加で分析していきたいと思います。

AICによるモデル選択（ステップワイズ法など）については、次回のR実践編で少し紹介されると思うので楽しみにしていてください。

参考文献