【初心者大歓迎!】線形回帰分析入門 ~ 最小二乗法から決定係数まで

今回は、統計分析の中でも基本的かつよく使われる線形回帰分析についての理論編です。
多少、数式も出てきますが、なるべく図や例を多く使って、直感的に分かりやすく伝えられればと思います。

この辺りについては、以下書籍でよくまとまっているので、よろしければ是非！

Pythonと実データで遊んで学ぶ データ分析講座

回帰分析とは

回帰分析とは、ある変数が与えられたとき、それと相関関係のあるの値を説明・予測することです。
例えば、を年齢、を年収としたときに、年齢が上がると年収がどれだけ上がるのか、
あるいは、ある年齢のときの年収はいくらかといったことが、回帰分析を使うことで分かります。

年齢が上がれば、年収が上がるなんて当たり前じゃん！と思うかもしれませんが、それを統計的に”○○万円上がる”（もしくは”○○円下がる”）と定量的に示せるところが回帰分析のいい所です。

線形回帰分析のイメージ

さて、以下のような年齢と年収に関するデータが与えられているとします。

年齢	年収
20	300
35	500
60	750
25	450
・・・	・・・

このようなデータを眺めていてもよく分からないので、ますは2次元にプロットしてみましょう。
（まずplotしてみてデータの分布を見てみることは、分析する上で大事なことです。）

なんとなく右上がりに点が偏っていますよね。
ただ、この図からだけだと、年齢と年収が相関してそうだ！！ということは分かりますが、年齢がどれだけ年収にインパクトを与えているの？（年齢が1歳上がったら、年収はいくら上がる？？）といった疑問には答えられません。

その疑問に答えるために、先ほどの図に以下のような直線を引いてみたいと思います。

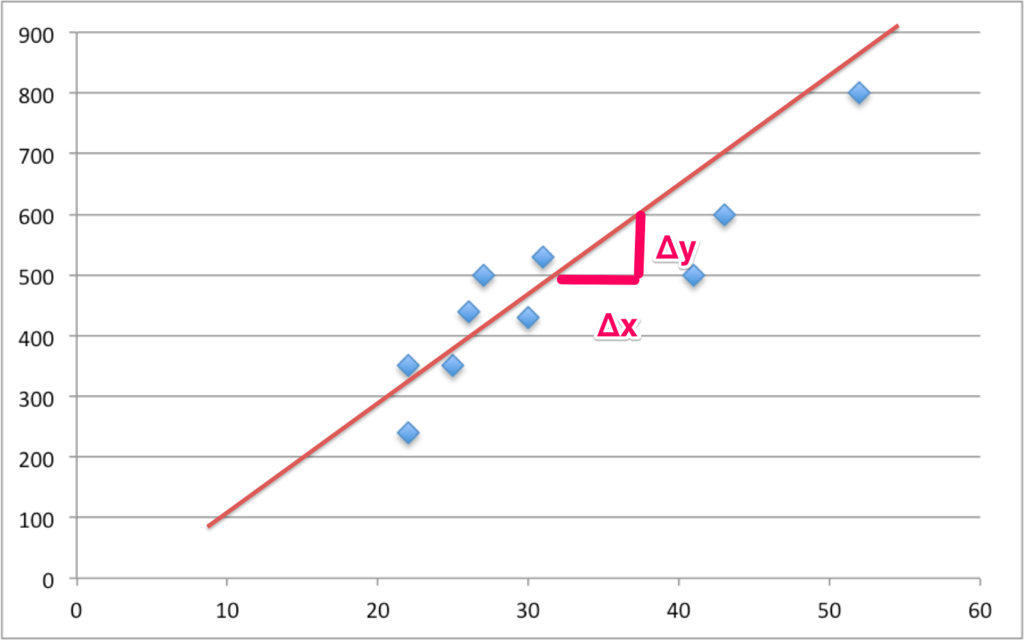
この直線から読み取れることは、xの変化量に対するyの変化量になります。
中学生で習った1次関数の式を思い出してみてください。
$$
y = ax+b
$$
とはパラメータです。

線形回帰分析でやりたいことは、ずばりこの1次関数を求めることにあります！
この1次関数が求まれば、が1単位変化したときのの変化量を求めることができ、先ほどの年齢が1歳上がったら年収がいくら上がるの？といったような疑問に答えることができます。
例えば、以下のようにパラメータが定まったとします。
$$
y = 15x+20
$$
このとき、(年齢)が1歳増えると、(年収）は15万円上がるといった感じになります。
また、年齢○○歳のときの年収も求めることができ、例えば、年齢が30歳の時、予測される年収は475万円です。

このようにして、年齢が年収に対して、どのくらい影響を与えているのかを定量的に分析することが可能です。
ここで、簡単な用語の整理ですが、を説明変数、を目的変数といいます。*1

また、上の例では説明変数が1つなので、単回帰分析と呼んだりします。
説明変数が2つ以上である場合は重回帰分析になります。

先ほどの例では線形関数（1次関数)を仮定しているので、線形回帰となりますが、非線形関数を仮定した場合は、非線形回帰になります。
この辺の用語はよく出てきますので、覚えておきましょう。

最小二乗法

さて、先ほどは適当に直線を引きましたが、どのような直線を引けば(どのようにパラメータの値を求めれば)良いのでしょうか？
観測データに最もあてはまりのよい直線を引けることができれば良さそうですが、正直わからないですよね。

そこで登場するのがOLS(最小二乗法)です。
以下の図を見てください。

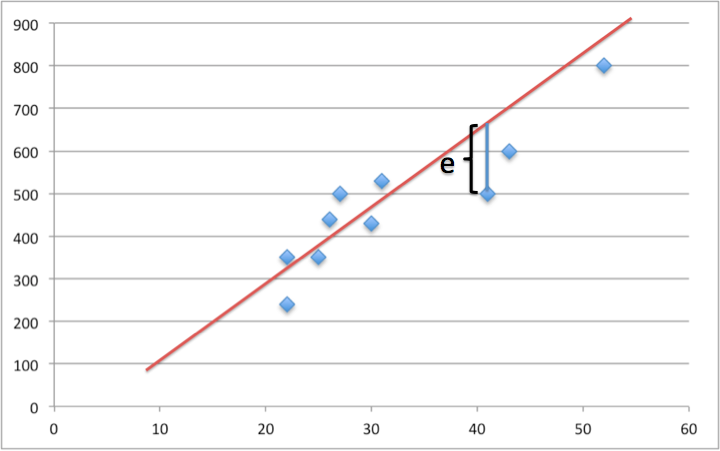
このeは、ある適当に引いてみた直線式と実際の観測値との誤差になります。この誤差を残差と呼びますが、各点における残差の和が最小となるようにパラメータを求める手法がOLSです。

OLSの数式展開

一応どのようにパラメータを求めるのか、数式展開を書きますが、
数式NG、なんとなくわかったからいいやという方は飛ばしてもらって構いません！！数式NGな方は、線形回帰では様々な直線が引けるなか、生まれた残差ができるだけ小さくなるような直線ができるようにパラメータを調節する、という認識をしてもらえればとりあえず大丈夫です。

直線の傾き、切片のパラメータを(a,b)とすると、i番目のデータについての残差\(e_i\)は、
$$
e_i = Y_i - aX_i - b
$$
となります。このままだと、残差がプラスであったりマイナスであったりして、扱いづらいため、2乗します。
残差二乗和（残差を2乗したものの和）は
$$
\sum_{i=0}^n {e_i}^2 = \sum_{i=0}^n (Y_i - aX_i - b)^2　\tag{1.1}
$$
となります。（標本サイズをnとしてる）
式(1.1)はパラメータ（a,b)の関数であり、OLSは、残差二乗和が最も小さくなるような（最も当てはまりのよいような）（a,b)求めることを目的としています。
最小化の一階条件として、式(1.1)をaとbで偏微分した値が0になる性質があるのでそれを用います。イメージとしては、
$$y = x^2 -2x + 1$$
のような二次関数が最小になる点は、をで微分した値が0になるとき（の傾きが0になるとき）、つまりのときですね。

それと同様に残差二乗和の式をやで偏微分をすることで効率よく求めることができます。
まず偏微分をしてみましょう。
$$
\begin{eqnarray*}
\frac{\partial \sum_{i=0}^n e_i}{\partial a} & = & -2\sum_{i=0}^n (Y_i - aX_i - b)X_i　\tag{1.2} \\
\frac{\partial \sum_{i=0}^n e_i}{\partial b} & = & -2\sum_{i=0}^n (Y_i - aX_i - b)　\tag{1.3}
\end{eqnarray*}
$$
次に、式(1.2)(1.3)の1階の条件（偏微分した値が0になるとき）は次のようになります。
$$
\begin{eqnarray*}
\sum_{i=0}^n (Y_i - aX_i - b)X_i　& = & 0　\tag{1.4} \\
\sum_{i=0}^n (Y_i - aX_i - b) & = & 0　\tag{1.5}
\end{eqnarray*}
$$
この2本の方程式は回帰の正規方程式と呼ばれます。

さて、(1.4)(1.5)の連立方程式を実際に解いてみましょう。
式(1.5)は、\(\overline{Y} - a\overline{X} - b = 0 \)となるので、bの解は、
$$
b = \overline{Y} - a\overline{X} \tag{1.5}
$$
となります。
式(1.5)を式(1.4)に代入すると、\(\sum_{i=0}^n(Y_i -\overline{Y} - a(X_i - \overline{X}))X_i = 0 \)となるので、
aの解は、
$$
a = \frac{\sum_{i=0}^n(Y_i -\overline{Y})X_i} {\sum_{i=0}^n(X_i - \overline{X})X_i } \tag{1.6}
$$
となります。
式(1.5)と(1.6)の式より、
$$
b = \frac{\sum_{i=0}^n(Y_i -\overline{Y})(X_i - \overline{X})} {\sum_{i=0}^n(X_i - \overline{X})^2} \tag{1.7}
$$
となり、X,Yの標本共分散をXの標本分散で割った形になっています。

ちなみに、上記の最小二乗法が使えるためには、誤差項に正規分布を仮定する必要があります。
正規分布については、下記リンクで簡単にまとめているので是非読んでみてください。
randpy.hatenablog.com

モデルの当てはまりの良さ？

モデルの当てはまりの良さとは、目的変数\(Y\)が説明変数\(X\)によってどれだけ説明できているかという意味合いです。
モデルの当てはまりが悪ければ、説明変数を追加するなどして、モデルを改良するための一つの指標になります。

以降では、モデルの当てはまりの良さを表す指標の一つである決定係数(\(R^2\))を導出してみます。
推定値と観測値の残差は\(e_i = Y_i - (aX_i + b)\)であり、式(1.5)を用いると以下のような式が得られます。
$$
Y_i - \overline{Y} = a(X_i - \overline{X}) + e_i \tag{1.8}
$$
この式の両辺を2乗し、iについて和をとってあげると、
$$
\sum_{i=0}(Y_i - \overline{Y})^2 = a^2\sum_{i=0}(X_i - \overline{X})^2 + \sum_{i=0}e_i^2 \tag{1.9}
$$
左辺は、全体の平方和(TSS)、右辺第1項は説明変数で説明される部分の平方和(ESS)、右辺第2項は残差平方和(RSS)になります。
ESSをTSSで割った値は、全体の平方和のうち説明変数で説明される平方和の比率を表しており、決定係数と呼ばれるものです。
$$
R^2 = \frac{ESS}{TSS} = 1 - \frac{RSS}{TSS} \tag{1.10}
$$
\(R^2\)(決定係数)は0~1までの値をとり、1に近ければ近いほどモデルの当てはまりが良いということになります。
どういう事かというと、例えば\(R^2\)が1になる場合は、式(1.10)のRSSがゼロになる時です。RSSは、残差二乗和ですから、これがゼロということは、直線上にすべての観測値がある事を意味しており、モデルの説明変数xでyを完全に説明できているということになります。

ちなみにモデル評価の指標として、\(R^2\)とは別に、\(AIC\)というものもありますが、それについては非線形回帰のセクションで紹介すると思います。

その求めた直線って何？

さて、今回求めた1次関数のパラメータは、
今回得られた標本を基に求まったものですが、
また別の標本でOLSを行えばパラメータの値は当然変わります。
以下の図をみてください。

たまたま得られた標本A,B,Cによるパラメータではなく、本当に求めたいのは母集団におけるパラメータです。

しかし、現実問題として、母集団のデータを得る事は不可能に近く、何らかの方法で標本で得られたパラメータと真に求めたいパラメータの誤差を評価する必要があり、そのために回帰分析を行う上では、実は様々な仮定をおく必要があります。
（撹乱項の期待値がゼロ、撹乱項が正規分布に従うなど）
この辺りは少し難しくなってくるので、今回はここまでに留めておきますが、引き続き、回帰分析の記事は上げていきたいと思いますので、その際に説明できればと思います！

終わりに

いかがだったでしょうか。今回は簡単な紹介しかできませんでしたが、
ざっくりとは線形回帰のイメージがついたのではないかと思います。

もっと深く勉強されたい方は、以下のような参考書が参考になると思うので、一度読んでみるといいかもしれません。
さて、次はR,Pythonを使って実際に線形回帰分析を行いたいと思いますので、お楽しみにー！

計量経済学 (y21)

統計学入門 (基礎統計学?)

*1:目的変数は、被説明変数、従属変数、また説明変数は独立変数などと呼ばれたりもします。