前回の記事では、決定木についてまとめました。
www.randpy.tokyo
今回は、前回チラッと触れた「木の剪定」について学んでいきましょう。
以下のような流れで進めていきます。
- 決定木の問題点
- 剪定・枝切りの考え方
- 正則化パラメータの決定の仕方
なお、前回同様参考図書としては、「はじめてのパターン認識」が良いかと思います。
- 作者: 平井有三
- 出版社/メーカー: 森北出版
- 発売日: 2012/07/31
- メディア: 単行本（ソフトカバー）
- 購入: 1人 クリック: 7回
- この商品を含むブログ (4件) を見る
剪定・枝切りを行わない場合の問題点
前回記事では、「誤り率・交差エントロピー・ジニ係数などで計算された不純度を最も減少させるように分割を進めていく」と説明しました。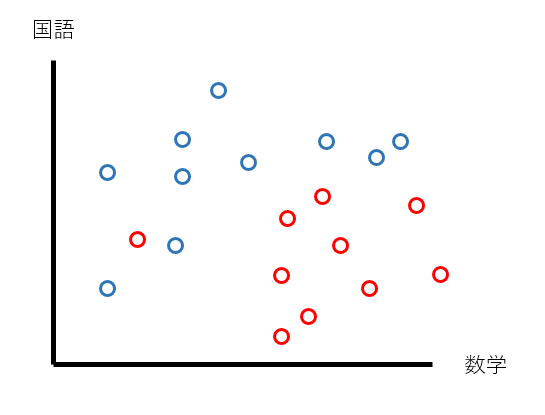
例えば、上の図を分割していくとしましょう。このグラフは、Aクラス（赤色）の生徒とBクラス（青色）の生徒を、国語と数学の点数によってプロットしたものです。
不純度が減少するように分割を進めると、以下のようになるでしょうか？
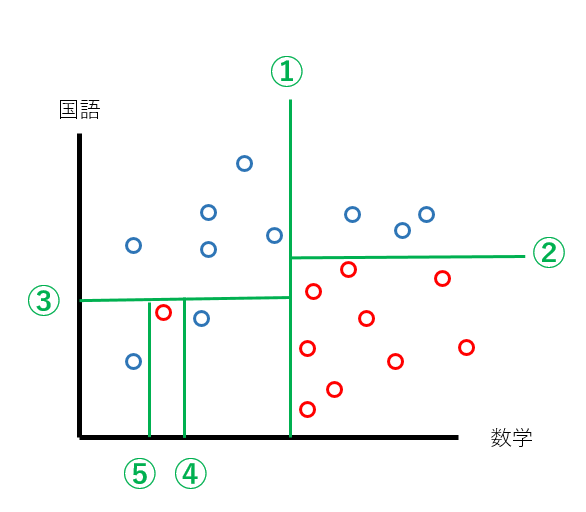
5回の分割を行うことで、やっと完璧に分類することができました。
この分割を木で表現すると、下のようになります。
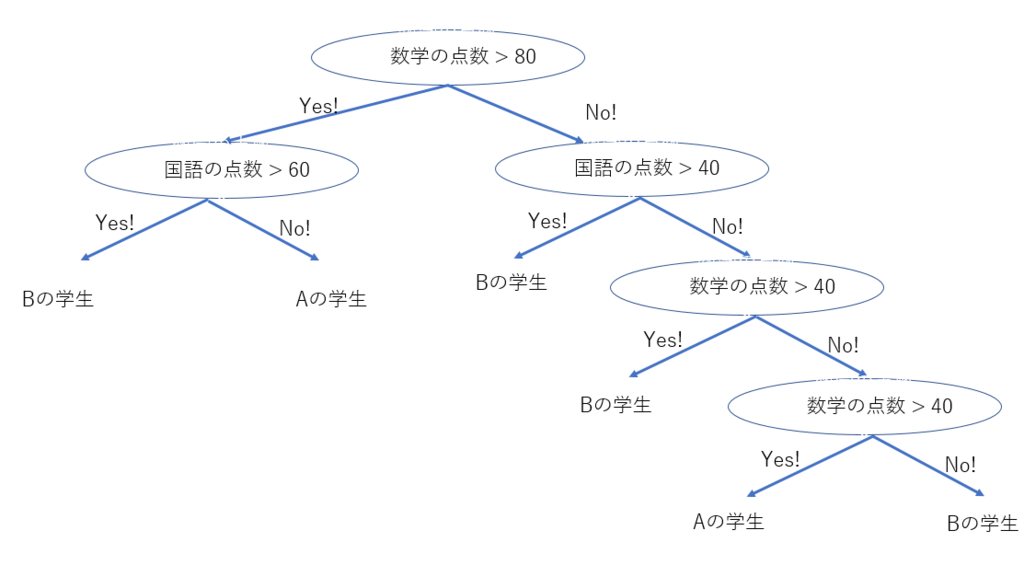
しかし、もう一度最初のプロット図を見ると、Aクラス（赤色）の生徒で一人だけ、ポツンと離れた位置にありますよね？
これはもしかすると外れ値かもしれません。
この外れ値があるがために、分割回数が多くなり、結果として木が大きくなってしまいます。木が大きくなるということは複雑性を持つということに繋がるため、できれば避けたいところです。
仮に、この外れ値を無視すると、分割回数は2回となり、
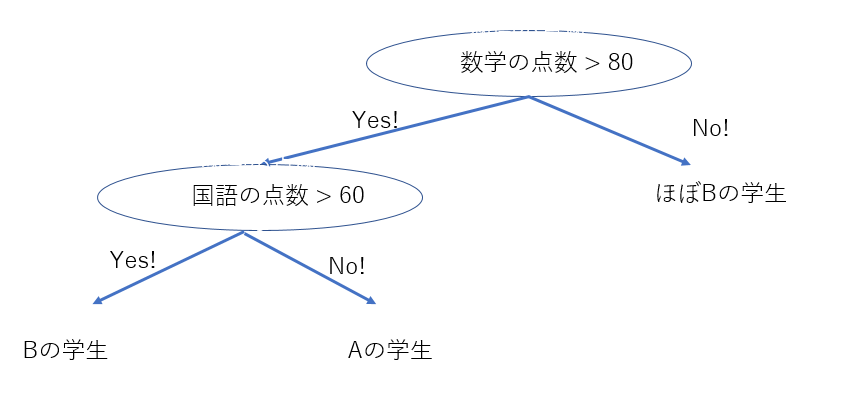
木は上のように非常にシンプルになります。
先ほどの木と比べると、右下の枝がバサッとハサミで切られたようになっています。
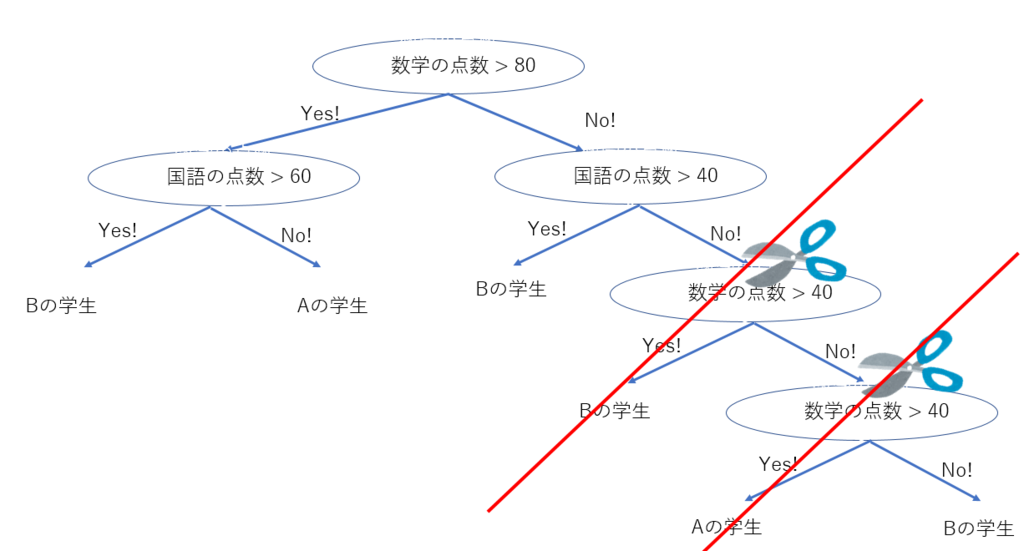
このような、木の下部分を切って元の木よりも小さくすることを剪定と言います。剪定、つまりは枝切りですね！
僕は剪定を行う際は、何故か頭の中であの芸人さんの「樋○カッター！！！」が毎回脳内再生されます…。はい、完全なる余談です。
この2つの木があった時に、どちらが汎用性があるかと言えば、恐らく後者でしょう。
前者の場合は、たまたま（かもしれない）現れたAの学生にとても影響を受けてしまい、別のデータでテストしてみると、全然役に立たない！ということが考えられます。
このように、分割回数を増やせば増やすほど、つまり木が大きくなればなるほど、厳密に分割できるようになる反面、汎用性が無くなってしまうというデメリットがあります。
分類の正確性・木の簡潔さ、どちらを取るか？
前節で、「分割回数を増やせば増やすほどいい」という訳ではないことが理解できたかと思います。しかし、だからといって「分割回数を少なくすればするほどいい」という訳でもありません。なぜなら、分割回数の減少はすなわち分類の不正確性をもたらすからです。
「分割回数をなるべく小さくしつつ（木をシンプルにしつつ）、分類をなるべく正確にしたい…」
という何とも我儘な要望を実現したいのです。
正則化パラメータと木のコストという考え
ここで、各終端ノード（そこから分割が起こっていないノード）の不純度をこの終端ノードが全体に与える不純度は、学習データの数で重みづけしてあげると、$$r(t)\frac{N(t)}{N}$$と表現できます。
この値を全ての終端ノードで計算してあげると、木全体の不純度を評価することができます。
$$R(T) = \sum_{t \in \tilde{T}}r(t)\frac{N(t)}{N}$$
ここで、終端ノードの数をとして、木の複雑性を
$$\alpha |\tilde{T}|$$と表現します。
このは、1つ終端ノードが増えるたびに、増加する木の複雑性を表したものと捉えるとスッキリするかもしれません。
木全体の不純度と、木の複雑性が数式を使って表現できたので、それらを組み合わせる以下のような数式が書けます。
$$R(T) + \alpha |\tilde{T}|$$
これを、木のコストと呼びます。
「うーん難しい…」という方のために、ここから具体例を使って説明していくのでご安心を！
具体例を使って、木のコストをイメージ！例えば、Aクラスの生徒とBクラスの生徒を分類する際に、下図のように2種類の木が作れるとします。
今回は、
、つまり終端ノードが1つ増えるたびに、木の複雑性が0.1増えるとします。
まず前者の木の不純度を求めると、（今回は計算が簡単な誤り率で不純度を計算していますが、前回やったジニ係数でも全く問題ないです！）
$$\bigl(1 - \frac{85}{95}\bigl)*\bigl(\frac{95}{200}\bigl) \\ + \bigl(1 - \frac{40}{45}\bigl)*\bigl(\frac{45}{200}\bigl) \\ + \bigl(1 - \frac{50}{60}\bigl)*\bigl(\frac{60}{200}\bigl) \\ = 0.125$$
となります。
この木の複雑性は、終端ノードの数が3つなので、$$0.1 *3 = 0.3$$
となります。
すると木のコストは、
$$R(T) + \alpha |\tilde{T}|\\ = 0.125 + 0.3 \\ = 0.425$$
と計算できます。
次に後者の木の不純度を求めると、
$$\bigl(1 - \frac{85}{95}\bigl)*\bigl(\frac{95}{200}\bigl) \\ + \bigl(1 - \frac{40}{40}\bigl)*\bigl(\frac{40}{200}\bigl) \\ + \bigl(1 - \frac{5}{5}\bigl)*\bigl(\frac{5}{200}\bigl) \\ + \bigl(1 - \frac{50}{60}\bigl)*\bigl(\frac{60}{200}\bigl) \\ = 0.1$$
となります。
この木の複雑性は、終端ノードの数が4つなので、
$$R(T) + \alpha |\tilde{T}|\\ = 0.1 + 0.1 *4 \\ = 0.5$$
と計算できます。
【分類の正確性】 = 【不純度の低さ】でいうと、後者の方が良さそうに見えるのですが、その分木が大きくなってしまっているので、
総合して木のコストを計算すると、前者の方が良い木と言えます。
また今回はとしましたが、次に
だとして計算を再度行ってみましょう。
すると、前者の木のコストは
$$R(T) + \alpha |\tilde{T}|\\ = 0.125 + 0.02 *3 \\ = 0.185$$
後者の木のコストは
$$R(T) + \alpha |\tilde{T}|\\ = 0.1 + 0.02 *4 \\ = 0.18$$
となり、今度は後者の方が良い木と判断されました。
今回の場合、とすると、両社の木のコストは一致します。よって
とすると前者の木の方が良い、
とすると後者の木の方が良い、ということが言えます。
このように、（終端ノードが1増えるたびに増加する複雑性）をどのような値に設定するかで、最終的に良い木は変わってきます。
を大きく設定すると、終端ノードが増えることが木のコストに与える影響も大きくなる → 分類が多少不正確でもなるべく小さい木が良い木と判断される。
という関係性があります。
実際にRやPythonで決定木を用いる際は、恐らく専用のライブラリを使うと思うので、その際に任意のを入力してあげれば、設定した
のもとでの決定木が自動で作られます。
なお、のような各要素の影響度合いを決定する変数を、正則化パラメータと呼びます。
どうやって正則化パラメータを決める？
では、どのように正則化パラメータもし、直観的に分かりやすくするために小さい木を求める場合は
しかし、それではあまりにデータ分析担当者の考えに偏ってしまうので、ここではK分割交差検証法（Cross-validation，クロスバリデーション）という方法を紹介します。
K分割交差検証法
K分割交差検証法では、まず手元のデータをK回繰り返すと、それぞれのデータセットを使って分析した際の、不純度（誤り率やジニ係数など）が計算できます。
それらを平均した値で評価すればよいわけです。
のときのK分割交差検証法から求められた平均不純度と、
のときのK分割交差検証法から求められた平均不純度と求め、より小さい方を選択すれば、より汎用的で別のデータに対しても精度が高いということが言えます。
パッケージを使って分析する際は、この辺りもKの数だけ与えあげれば勝手に最適なを教えてくれます。
ただ説明を読んでもイメージが付きにくいかもしれませんので、実践記事にて改めて説明することにします。
今は「こういう評価方法があるんだなー」ぐらいの理解で大丈夫です！
ちなみにK分割交差検証法は決定木限らず、様々な手法を評価する際に使われています。
終わりに
今回は、前回の決定木入門編 「ウォーリーを探せ」から考える不純度の考え方で紹介しきれなかった木の剪定について説明しました。今回の記事にて、決定木の説明は一旦以上とさせていただきます。
次回は、決定木を応用したランダムフォレストという手法を紹介する予定です。
ランダムフォレストは、アイデアとして非常にシンプルにも関わらず、高い精度が出ることで知られています。
ランダムフォレストの理論記事公開後、何らかのデータを決定木とランダムフォレストを使って分析する予定です！
決定木やランダムフォレストの実践はとても面白いと思います。
お楽しみにー！！
