ポアソン分布：ある時間帯にかかってくる電話の数がわかる！？？

今回は、ポアソン分布についてやっていきます。
こちらの確率分布も非常に重要ですので、頑張って理解していきましょう。

関連する分布としては二項分布があるので、それについては以下の記事を参考にしてみてください。
randpy.hatenablog.com

ポアソン分布って何？？

ポアソン分布は、単位時間内、あるいは単位空間内において、ある事象が何回生じるかという偶然のメカニズムを表す確率分布です。

？？？

ポアソン分布が当てはまる現象は数多く存在するので、具体例を出して考えましょう。
例えば、ある地域内における1日の交通事故件数、ある会社の電話機に午後2時~3時の間でかかってくる電話の数、ある野球チームの1試合あたりのホームラン数などです。
これらの現象に共通していることは、「なかなか起こりにくい」という点です。（自宅近くの交通事故ってそんなに起きないですよね？）

こうした偶然性の高い現象を説明するのにポアソン分布がよく使われます。

ちなみに歴史的に有名なところでは、ボルトキーヴィッチの「プロシア陸軍において馬に蹴られて死んだ兵士の数」が挙げられ、ポアソン分布が最初に応用された事例と言われています。

さて、続いてはポアソン分布の確率質量関数について見ていきましょう。
単位時間内、単位空間内で生じるある現象の生起回数をx回とし、xがポアソン分布に従うと仮定すると、xの確率分布は以下のようになります。

$$
\mathcal{f}(x) = \frac{\lambda^{x} e^{-\lambda}}{x!}
$$

ちなみにこの式は、二項分布において、\(np=\lambda\)(\(\lambda\)は一定)とした時にnを限りなく大きくする（ｐは小さくなる）ことで導くことができます。

詳しい導出は割愛しますが、nは二項分布における試行回数なので、試行回数をめちゃくちゃ増やしても（n→∞)、滅多に起こらない(p→0)事象に対してポアソン分布が使われるとイメージして頂ければ大丈夫です。

ポアソン分布の期待値と分散

ポアソン分布の期待値と分散ですが、結論としては両方ともパラメータ(\(\lambda\)になります。
期待値と分散を実際に導出してみましょう。
数式展開をひたすらするだけなので、飛ばしてもらっても構いません。

最初の準備として\(e^x\)の0のまわりでのテーラー展開を使います。

$$
e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + … = \sum_{k=0}^∞ \frac{x^k}{k!}
$$

これを使って期待値を計算すると以下のようになります。

\begin{eqnarray*}
E(X) & = & \sum_{x=0}^∞ x \frac{\lambda^{x} e^{-\lambda}}{x!}\\
& = & e^{-\lambda}\sum_{x=1}^∞ \frac{\lambda^{x}}{(x-1)!}\\
& = & \lambda e^{-\lambda}\sum_{x=1}^∞ \frac{\lambda^{x-1}}{(x-1)!}\\
& = & \lambda e^{-\lambda} e^{\lambda} = \lambda\\
\end{eqnarray*}

分散は少し工夫が必要で、以下のような式を考えます。

\begin{eqnarray*}
var(X) &=& E(X^2) - [E(X)]^2\\
&=& E[X(X-1)] + E(X) - [E(X)^2]
\end{eqnarray*}

このように分散の式を分解できます。\(E(X)\)は既に求まっているので、あとは\(E[X(X-1)]\)を求めれば分散が求まります。

\begin{eqnarray*}
E[X(X-1)] & = & \sum_{x=0}^∞ x(x-1) \frac{\lambda^{x} e^{-\lambda}}{x!}\\
& = & \lambda^{2}e^{-\lambda}\sum_{x=2}^∞ \frac{\lambda^{x-2}}{(x-2)!}\\
& = & \lambda^{2}e^{-\lambda}e^{\lambda} \\
&=& \lambda^{2}\\
\end{eqnarray*}

これで必要な計算は終わったので、あとは先ほどの分散の式に代入していくだけです。

\begin{eqnarray*}
var(X) & = & E[X(X-1)] + E(X) - [E(X)^2] \\
&=& \lambda^{2} + \lambda - \lambda^{2} \\
&=& \lambda \\
\end{eqnarray*}

ポアソン分布の期待値と分散がパラメータ\(\lambda\)になることは特徴の一つなので、余力のある方は覚えておきましょう。

ポアソン分布の形状

ここからはポアソン分布がどのような形か実際に見ていきましょう。
コードの記述はPythonで書いていきます。（Rユーザーの方もRを使って試してみてください。）

まずは、ポアソン分布がどのような形になっているのかプロットしてみましょう。
ポアソン分布に従う乱数を1000個用意して、(\(\lambda\)の値を変えた時の分布を出してみます。

from scipy.stats import poisson
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

#ポアソン分布に従う乱数発生 size固定
arr1 = np.random.poisson(lam = 1, size = 1000)
arr2 = np.random.poisson(lam = 4, size = 1000)
arr3 = np.random.poisson(lam = 10, size = 1000)

# plot
plt.hist(arr1, label='$\lambda$=1', bins=20, range = (0,20), alpha = 0.5, color='blue')
plt.hist(arr2, bins=20, label='$\lambda$=4', range = (0,20), alpha = 0.5, color='red')
plt.hist(arr3, label = '$\lambda$=10', bins=20, range = (0,20), alpha = 0.5, color='green')
plt.legend()

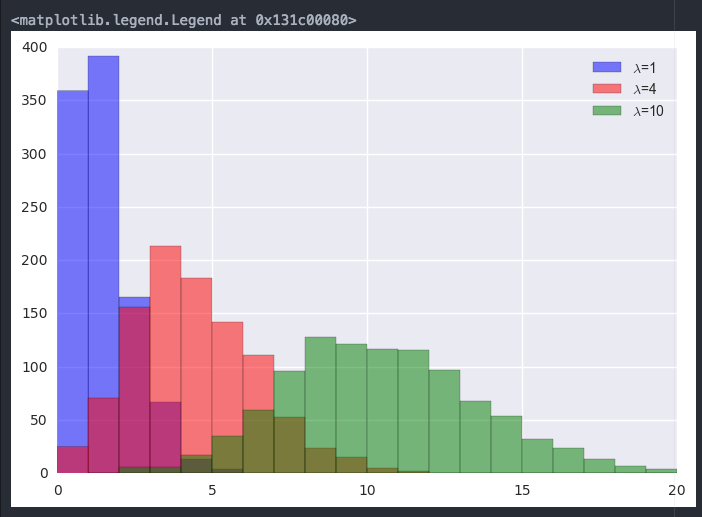
\(\lambda=1\)（青色）の分布を見てみると、生起回数0回、1回が多く、2回を超えてくると途端に生起回数が減少していますね。

これは、単位時間内に平均1回事象が発生するポアソン分布を仮定したおき、単位時間内に3回、4回と複数回起こる確率が低いことを示しています。
また、\(\lambda\)が1,4,10と大きくなるにつれて、分布が右にスライドしていってるかと思います。
\(\lambda\)はポアソン分布の平均であるので、それを中心とした分布の形になります。

ちなみに、\(\lambda\)が大きくなるにつれて\(\lambda\)を中心とした山型の分布になっていることにお気づきでしょうか？
この山型の分布、どこかで見覚えがありますよね？
そうです。正規分布です。
\(\lambda\)が十分大きい時、\(N(\lambda , \sqrt[]{\lambda})\)の正規分布に近似することができます。

正規分布というのはデータ分析をする上で非常に使い勝手がいいので、
近似できる場合は、正規分布として扱うことが多いです。

この辺りは今後の分析の中で出てくるかと思うので、その際にまた説明できればと思います。

午後4時から5時の間にかかってくる電話の数は？？

さて、ポアソン分布を使って何ができるの？ということになりますが、
例えば身近な例を出すと、
会社の電話機に、ある時間帯に何回電話がかかってくるのか、ある程度予測することができます！
（できたところで何それって感じですが……）

それでは実際にやってみましょう。
午後4時から5時の1時間の間に平均3回電話がかかってくることが分かっているとします。

これで\(\lambda\)の値が決まったので、あとはポアソン分布に当てはめていくだけで、電話数に応じた確率を求めることができます。

試しに5回電話がかかってくるときの確率を求めてみましょう。
確率質量関数から手計算で出してもいいですが、正直面倒なので、pythonで求めちゃいます。
scipyのpoissonというライブラリを使って計算します。

from scipy.stats import poisson
lam = 3
poisson.pmf(5,lam)*100

計算してみると、5回電話がかかってくる確率は10.1%となります。

さて、5回かかってくる確率は出せましたが、例えば5回以上電話がかかってくる確率はどのくらいなのでしょうか。
これは、累積分布関数を求めれば計算できます。

lam = 3
1 - poisson.cdf(4, lam)

電話が4回以内の確率を出して、1からその確率を引くことで、5回以上電話がかかってくる確率を求めることができます。
実際に計算してみると18.5%ほどになります。

平均3回でも、5回以上の電話がかかってくることは十分にあるので気をつけないといけませんね。

このような身近な現象について、ポアソン分布を当てはめることが可能なので、ぜひ試してみてください。

さいごに

今回はポアソン分布について紹介しました。
少し数式が出てきて混乱した方もいるかもしれませんが、単位時間内、単位空間内において滅多に起こらない事象に対してよく当てはまる確率分布というところだけ覚えておいて頂ければ今回は良しとしましょう！

ちなみに、うちの実家は自営業なんですが、1日あたりの来客数がポアソン分布によく当てはまりそうです、、、悲しい。

確率分布については今後も紹介していくかと思いますが、詳しく知りたい方はぜひ以下の文献などで調べてみてください。

統計学入門 (基礎統計学?)

統計学入門