統計学をやるうえで、確率分布を考えることは非常に大切です。
線形回帰でよく用いられるOLS(最小二乗法)という手法がありますが、これはデータが正規分布に従うことを仮定しています。
正規分布に従わないデータを持ってきて、正規分布を仮定した手法を用いても、結果はとても怪しい推定となるでしょう。
しかし、私が学生時代に卒業研究などで見た発表などは、特に確率分布について考えずに、いきなりOLSしているというものが多くありました。
今回は、そこからステップアップするために、確率分布の中でも基本となる正規分布について説明します。
※追記※
スマホだと数式がうまく表示されない可能性がありますので、こちらのリンク、もしくはPCから購読頂けますと幸いです。
正規分布
正規分布についてできるだけ簡単に一言で説明すると、「平均値の近くに多く数があり、平均値から離れれば離れるほど数が少なくなるようなデータを表す確率分布」という文章になるでしょうか?画像をお見せしたほうが早いかもしれません。

この横軸がデータの取る値、縦軸がそのデータが起こりうる確率の高さを表すと考えてください。
この
あたりが最も起こりやすく,
あたりはほとんど起こらないということを意味しています。
正規分布の具体例と正規分布に当てはまらない具体例
よく言われている正規分布の例が身長です。
上記の正規分布の画像例は、日本人の女性の身長の分布に近いかもしれません。
150cmぐらいの身長の方が最も多く、150cmから離れるほど(150cmよりも小さい or 150cmよりも大きい)、そのような方の人数は少なくなる、ということです。何となく想像がつくのではないでしょうか?
また図からもわかるように、正規分布に従うデータの場合、中央値と平均値は一致します。
つまり、例えば99人の人たちを背の小さい順に並べて、中央値(50番目)の人の身長を測ると、だいたい平均値と一致するということになります。
また図から、もしくは現実の人を思い浮かべても、平均と離れていても160cmぐらいの人はある程度の数いますが、170cm以上となると人数は一気に減ります。これも正規分布の特徴で、平均からある程度離れると、起こりうる確率がカクンと減ります。
他に正規分布に従うと言われる例として、試験の点数の分布などがあります。
正規分布に従わない例
逆に正規分布に当てはまらないものに、年収の分布があります。Web上で定期的に「平均給与」について話題になりますが、「えっ!そんな高いの?私低すぎるかも!」と驚くことが多いのでないでしょうか?
例えば国税庁が発表している、日本人の平均給与は414万円です。
「えっ!そんな高いの?私低すぎるかも!」と思ってしまう方が多いのは、「必ず平均値 = 中央値である」と勘違いしているからです。
確かに正規分布であれば平均値と中央値が一致しますが、そうでないデータももちろんあります。
実際には平均から大きく離れた、年収を1000万以上稼ぐ人は一定数いますし、また2000万以上、そしてそれ以上(自分とかけ離れすぎて想像したくない……。)稼ぐ人もいます。
グラフにすると以下のようなイメージです。
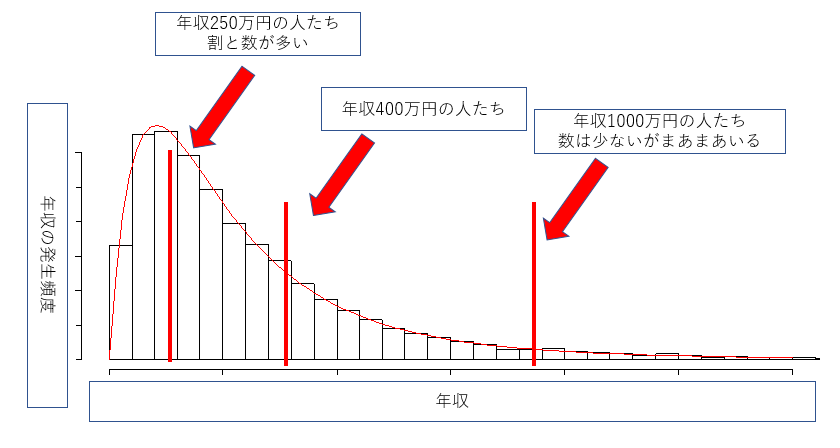
あくまで直観的に分かりやすいイメージしやすい図を作成したため、もちろん正確な図ではないので注意してください。
見てもらうと、先ほどの正規分布の形とは違いますよね。
平均から離れても、ある程度発生確率が高いまま保たれています。
このようにある一定のバカみたいに稼ぐ人たち(悔しいので少し嫌な表現にしてみました)によって、平均が人々の予想よりも高くなってしまっている場合、
単純に平均値を代表値として考えるのは直観的に合わないケースが生じます。
このような点からもデータの分布を考えることの重要性が見えてきます。
正規分布を数式で書くと……
これまで直観的な話を中心にしてきましたが、最後に数式を紹介します。正規分布の形を決定するのは
:平均
:標準偏差
この2つの変数です。
平均は文字通りデータの平均を求めたもの。標準偏差はデータのバラつき具合を表す数値となります。
平均・標準偏差・分散のあたりの計算については、別記事について改めて紹介する予定ですので、もう少々お待ちください。
今は「データがどれほどバラついているかを表すのが標準偏差」と認識していれば十分です。
つまり、標準偏差が小さければ、データが平均値周りに集まっていて、反対に標準偏差が大きければ、データが平均から離れたところにも起こりやすい、ということになります。
これら「平均と標準偏差」を用いて正規分布を数式を使って表すと、
となります。
左辺の数式は、平均 と標準偏差
が与えられたときの、正規分布に従う確率変数
が起こる確率(正確には確率密度関数)を意味しています。
右辺はその関数の形です。
平均と標準偏差を変えながら図を描いてみる
先ほどの平均と標準偏差から正規分布の形が決まる、という話ですが、少しややこしく感じた方もいるかもしれません。そこで、平均と標準偏差を少しいじりながら、図をみて直観的に理解してみたいと思います。
まずは先ほどあげた例ですが、

これは平均150、標準偏差6のグラフをRにてプロットしたものです。
次に平均150、標準偏差10のグラフを描いてみます。

少し幅が広がりましたね!標準偏差が大きくなる = データの平均からのばらつきが大きくなる、ということだったので135や165あたりもある程度データがあることが分かります。
続いて平均160、標準偏差10のグラフを描いてみます。
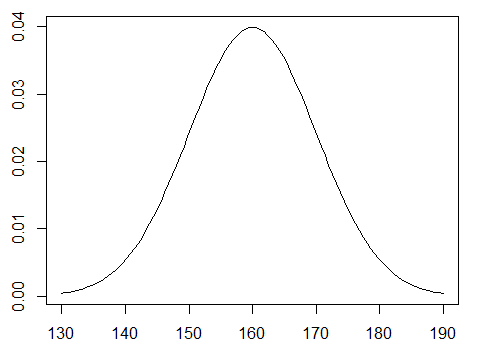
中心の部分が150から160に移動しました。
こんな風に平均と標準偏差によって正規分布の形が決まります。
ちなみにこの正規分布の図を描くためのRのコードですが、以下の通りです。
curve(dnorm(x,160,5),130,170) curve(dnorm(x,160,10),130,170) curve(dnorm(x,160,10),130,190)
dnorm(x,160,10)
の部分を色々変えて様々な正規分布の形を実際に見てみましょう!
正規分布の便利な性質
最後に正規分布に従うデータの場合に、便利な性質があるので紹介します。- 平均 ± 標準偏差 の間にデータの約68.3%が含まれる
- 平均 ± 2 × 標準偏差 の間にデータの約95.4%が含まれる
- 平均 ± 3 × 標準偏差 の間にデータの約99.7%が含まれる
という性質です。
これは大変便利で、例えば身長のデータが平均150cm、標準偏差5cmの正規分布に従うと分かっているとします。
このとき、
- 145cm ~ 155cmの中に68.3%ぐらいの人がいる
- 140cm ~ 160cmの中に95.4%ぐらいの人がいる
- 135cm ~ 165cmの中に99.7%ぐらいの人がいる
ということが分かります。
これを知っておくと、大体値がどの範囲に収まるが暗算でも計算できちゃいます!
最後に
正規分布についての説明は以上となります。今回はなるべく直観的理解にとどめようと頑張ってみました。
今後少しずつ加筆していき、もう一歩理論の方に踏み込んだ話も書いていく予定です!
また正規分布以外にも重要な分布、例えばポアソン分布や二項分布もあるのでそのあたりも近日中に執筆していこうと思います。
乞うご期待!