機械学習の分野でよく使われる決定木について今回は説明していきます。
決定木は、回帰、分類問題に対して、非常によく使われる手法の一つで、あらゆる現場でよく使われているのではないかと思います。
アルゴリズム自体はとてもシンプルですし、R,Pythonにおいてパッケージも豊富というところもあり、
何よりも結果の可読性の高さが人気の一つの理由かと思います。
今回の進め方としては、以下のように進めていきます。
- 決定木って何?(ざっくり図から理解)
- 分割規則(不純度について)
決定木の理論面については、「はじめてのパターン認識」を参考にしていただくといいかと思います。

- 作者: 平井有三
- 出版社/メーカー: 森北出版
- 発売日: 2012/07/31
- メディア: 単行本(ソフトカバー)
- 購入: 1人 クリック: 7回
- この商品を含むブログ (5件) を見る
決定木とは
決定木は、条件分岐によってグループを分割して分類する手法です。
その際にグループがなるべく同じような属性で構成されるように分割します。
例えば、以下のようなプロットがあったとします。
これは、ある2つの学校AとBの生徒の数学と国語の点数の分布です。(右にいくほど数学の点が高く、上にいくほど国語の点数が高い)
なお、Aの学生は赤、Bの学生は青でプロットしています。
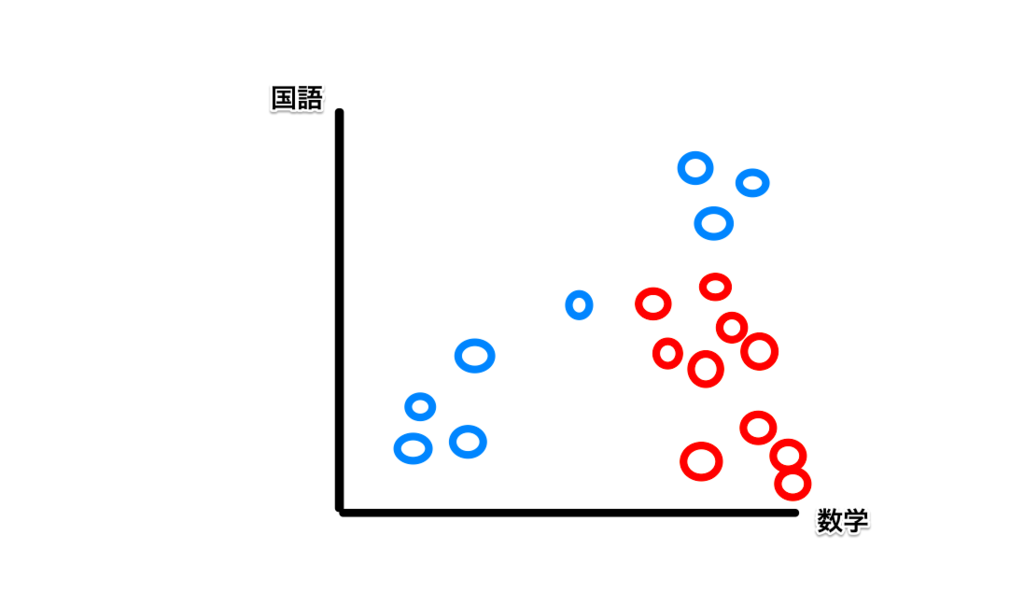
2つの学校の生徒を分類するにはどうしたらいいのでしょうか。
例えば、数学の点数(横軸)で80点(仮)を境にして区切ってみると、80点以上が学校Aと学校Bの生徒のグループ、80点未満が学校Bの生徒のグループにざっくりと分割することができた思います。
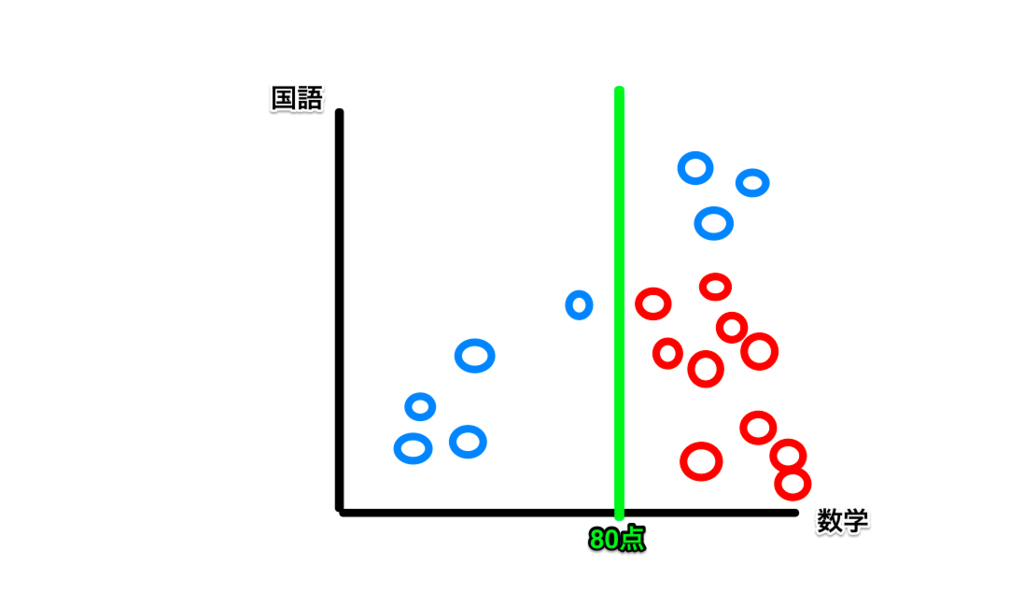
数学80点以上にAとBが混ざっているので、今度は、国語の点数に注目して、国語60点を境にしてみると、AとBを完全に分けることができます。
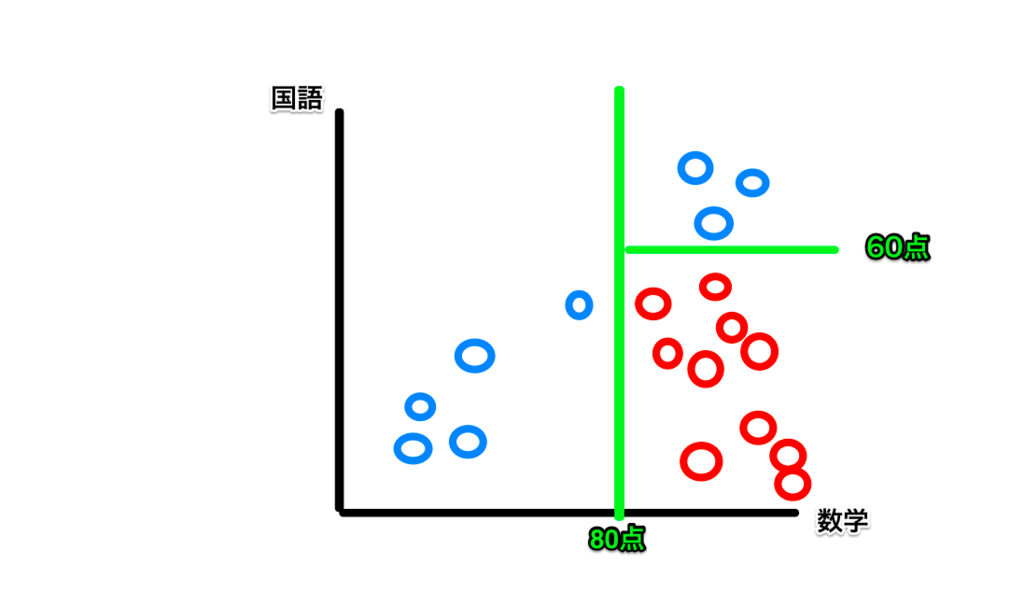
今の流れを図に表すと次のようになります。

このように条件分岐を繰り返すことで、上図のようにツリー状にどんどん展開されていきます。
この見た目が木のようであることが、決定木と言われる所以です。
さて、ここでいくつかの疑問を持った方もいるかと思います。
- 分割の基準(今回でいう点数)はどうやって決めるの?
- 数学からじゃなくて国語から分割しちゃだめなの?
- 数学、国語以外に物理、化学など他にも多くの特徴量があったときの分割の規則は?
などなど、疑問がたくさん浮かんだかと思いますので、その辺りについては次の章で紹介する不純度という考え方で解決していきたいと思います。
不純度の考え方
決定木では、不純度という指標をもとに分割します。
色々なクラスが混在するグループは不純度が高く、ある一つのクラスで構成されている、もしくはある1つのクラスの割合が大多数を占めるほど不純度は低くなります。
決定木では、分割後のグループの不純度が一番小さくなるような基準を選んで分割していくというのが基本的な流れです。
不純度が小さくなるという部分が少し分かりづらいと思うので、ここで「ウォーリーを探せ」に例えてみます。
ウォーリーを探せで遊ぶ際に、
- 紙面の右と左で分割して探す
- 紙面の上下で分割して探す
- 赤と白のボーダーを着ているかどうかで分割して探す
の3つの方法を思いついたとします。
どの分割方法がいいか考えたときに、
1,2の分割方法では、分けた二つのグループにあまり違いがでませんが、3(赤白ボーダー)で分けることで、分割後のグループに特徴をもった集団が固まり、情報がすっきりします。
このように分割後のグループがある集団で固まっている=不純度が小さいほど、良い分割基準を選べているということになります。
さて、これまでざっくりと「不純度」と表現していましたが、それってどうやって計算してあげたらいいの?という疑問が浮かびそうです。
不純度を表す代表的な関数として、以下のものが挙げられます。
tをノード、
1. 誤り率
$$
E(t) = 1 - \max_i{P(C_i|t)}
$$
2. 交差エントロピー
$$
E(t) = -\sum_{i=1}^{K}P(C_i|t)lnP(C_i|t)
$$
3. ジニ係数
$$
E(t) = 1-\sum_{i=1}^{K}P^2(C_i|t)
$$
ただ、これだけだと正直よくわからないので、実際にジニ係数を計算して、不純度の違いをみていきます。
学校A、Bそれぞれ100人ずつの計200人いる状態から、2つのルールで分割した場合の結果が以下のようになったとします。
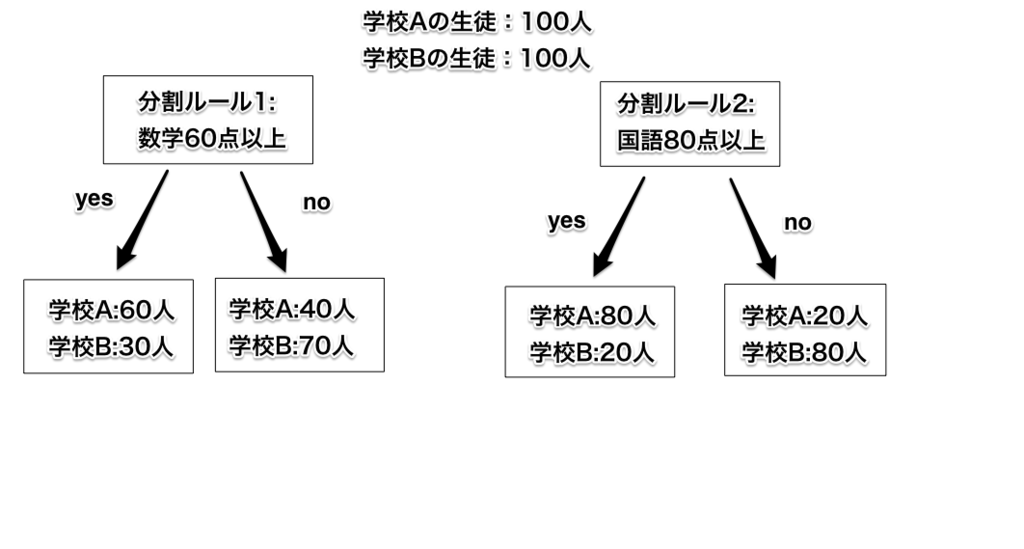
分割ルール1の'yes'グループのジニ係数は、
\[1 - \bigl((\frac{60}{90})^2 + (\frac{30}{90})^2\bigl) = \frac{4}{9}\]
分割ルール1の'no'グループのジニ係数は、
\[1 - \bigl((\frac{40}{110})^2 + (\frac{70}{110})^2\bigl) = \frac{56}{121}\]
となります。
これらをもとに、生徒の数で重み付けしてあげると、分割ルール1による不純度は
\[\frac{90}{200}ジニ係数(yes) + \frac{110}{200}ジニ係数(no)\]
となります。
分割後の不純度が計算できたので、分割前の不純度との差は、
\[ジニ係数(分割前) - \frac{90}{200}ジニ係数(yes) - \frac{110}{200}ジニ係数(no)\]
という式で表せます。実際に計算してみると不純度の差分は0.0454となります。
同様に分割ルール2でも不純度の差分を計算してみると、0.18となります。
この差分を様々な分割ルールで計算し、差分の大きいもの、つまり最も不純度が減少したルールを適用すれば良いわけです。今回の例では分割ルール2を採用したほうがいいということになります。
まぁ図の数値をみただけでも分割ルール2の結果の方がよく分類できていることはすぐにわかるかと思いますので、直感的にもあってる結果が出ているかと思います。
決定木の手法
さて、さきほど不純度の指標をいくつか説明しましたが、これらは、決定木の手法によって使い分けられます。代表的なものとしては以下のものが挙げられています。
- CART
−2分木のみの分割(一回の分割で2つまで)
−ジニ係数、エンロトピーを分割基準
- C 4.5
−多分木による表現も可能(一回の分割で2つ以上の分割が可能)
−エントロピーの違いによって分割(情報利得比を基準)
決定木と剪定
大方の決定木の流れはわかったかと思いますが、どこで分割をやめればいいのかが一つ重要なポイントになります。基本的には、できるだけ1つのクラスのグループができるまで木を成長させ、そのあと木の剪定を行います。
木が大きくなると汎化誤差が大きくなり、過学習を引き起こしてしまい、「新しいデータで試した時に全く通用しない」なんてことが起こりえます。
そこで、精度は高く、かつより汎用的な木を作るために、ある程度の木の深さで成長を止めてあげるこことが重要になります。
木の剪定については以下で説明しています。よろしければこちらもご覧ください。タイトルはちょっと煽ってますが、内容はまじめです…笑。
www.randpy.tokyo
終わりに
今回は決定木について簡単に説明しました。(適宜補足は付け加えていきます)
決定木は大変便利な手法ですが、学習データが少し変化しただけで識別器の性能が大きく変わってしまいます。
そういった問題点を克服するために、バキング、ブースティング、ランダムフォレストといったアンサンブル学習の手法があるので、これらについては次回の理論編で書きたいと思います。
さて、決定木分析の実践編、、、データに何を使うか悩み中ですがこれまで通りRとPythonで分析していきたいと思いますのでお楽しみにー。
(最近更新頻度が少し落ち気味なので、これからペースアップしていきます!!)